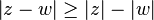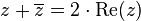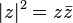Hola Bienvenido a este nuevo blog...
Aquí esta toda información sobre los números complejos espero que te sirva.
Un poco de Historia: La resolución de ecuaciones algebraicas ocupó a los matemáticos desde los tiempos de los antiguos egipcios y babilónicos, quienes desarrollaron métodos para resolverecuaciones lineales y cuadráticas. Estas ecuaciones, formuladas verbalmente en aquel entonces y no a través de los símbolos que hoy utilizamos, surgieron de las necesidades prácticas propias de actividades como el comercio y las finanzas por un lado y la agricultura y la medición de terrenos por el otro. El estudio de las ecuaciones lineales del tipo: donde | ||||
| exige, para su solución, que se consideren los números negativos. Estos números fueron utilizados en India y China varios siglos antes que en Europa. | ||||
Análogamente, las ecuaciones del tipo: | ||||
| donde | ||||
| ||||
El conjunto de los números naturales se va ampliando así, de manera que, para diferentes tipos de ecuaciones se pueda garantizar la existencia de una solución dentro de los conjuntos 'ampliados': Si
donde el símbolo
| ||||
| Ya desde los tiempos de los pitagóricos se reconoció la existencia de números no racionales; cuando se intentó calcular la medida de la diagonal de un cuadrado de lado 1, con el uso del Teorema de Pitágoras. |
| |||
| se concluyó que | ||||
| La solución, que hoy denotamos por | ||||
Ahora bien, en la resolución de ecuaciones cuadráticas, durante la Edad Media y antes, se ignoraban los casos como el siguiente: | ||||
| Al intentar usar la fórmula: | ||||
| Se obtiene: | ||||
| Sabiendo que ningún número elevado al cuadrado es igual a | ||||
| Sin embargo, muchos años más tarde, en el siglo XVI, en pleno Renacimiento europeo, el matemático italiano Girolamo Cardano, haciendo grades esfuerzos por encontrar fórmulas para la resolución de las ecuaciones de grado 3 y de grado 4, descubrió que era útil considerar las raíces cuadradas de números negativos 'como si fueran números', y operar con ellas tal y como lo haría con números verdaderos, a pesar de que, según propias palabras, había que ser capaz de 'soportar la tortura mental' que esto significaba. |  | |||
Es así como se inicia el tratamiento de los números que ahora llamamos 'complejos': como una especie de 'truco' para resolver un problema algebraico, truco que para su propio creador resultaba ser una tortura mental. Han pasado varios siglos desde entonces, y ya los números complejos no deberían representar una tortura para nadie. Han sido aceptados y debidamente estudiadas sus propiedades. Se han encontrado mútiples aplicaciones o usos de los números complejos, especialmente en la Física y particularmente en la Electricidad. | ||||
¿Que son los números complejos?
Los números complejos constan de dos componentes: una parte real y una imaginaria. Cuando estamos representando números complejos, llamamos "eje real" al horizontal y "eje imaginario" al vertical. Un punto de un plano se puede expresar como número complejo . Lo importante es tener en cuenta que un número complejo puede representarse gráficamente como un vector, por eso conserva de éste sus coordenadas polares: el módulo y el ángulo.
Un número complejo describe la suma de un número real y un número imaginario (que es un múltiplo real de la unidad imaginaria, que se indica con la letra i). Los números complejos se utilizan en todos los campos de las matemáticas, en muchos de la física y en ingeniería. Los números complejos describen la suma de un número real y un número imaginario (que es un múltiplo real de la unidad imaginaria, y se indica con la letra i). Los números complejos se utilizan en todos los campos de las matemáticas, en muchos de la física (particularmente en la mecánica cuántica) y en ingeniería, especialmente en la electrónica y las telecomunicaciones. Esta utilización generalizada se debe a su utilidad para representar las ondas electromagnéticas y la corriente eléctrica.

Aquí esta un vídeo con una mejor explicación de los números complejos y conceptos básicos y también unos ejercicios básicos:
Operaciones con los números complejos | ||
Se definen las operaciones de suma, resta, producto y división en el conjunto de los números complejos de la siguiente manera:
Suma: Si Por ejemplo, | ||
Resta: Siendo
Por ejemplo: | ||
Cuerpo de los números complejos
Los números complejos forman un cuerpo, el cuerpo complejo, denotado por C (o más apropiadamente por el carácter unicode ℂ ). Si identificamos el número real a con el complejo (a, 0), el cuerpo de los números reales R aparece como un subcuerpo de C. Más aún, C forma un espacio vectorial de dimensión 2 sobre los reales. Los complejos no pueden ser ordenados como, por ejemplo, los números reales, por lo que C no puede ser convertido de ninguna manera en un cuerpo ordenado.
Unidad imaginaria
Tomando en cuenta que  , se define un número especial en matemáticas de gran importancia, el número i o unidad imaginaria, definido como
, se define un número especial en matemáticas de gran importancia, el número i o unidad imaginaria, definido como
 , se define un número especial en matemáticas de gran importancia, el número i o unidad imaginaria, definido como
, se define un número especial en matemáticas de gran importancia, el número i o unidad imaginaria, definido como
De donde se deduce inmediatamente que,
Valor absoluto o módulo, argumento y conjugado
Valor absoluto o módulo de un número complejo
El valor absoluto, módulo o magnitud de un número complejo z viene dado por la siguiente expresión:
Si pensamos en las coordenadas cartesianas del número complejo z como algún punto en el plano; podemos ver, por el teorema de Pitágoras, que el valor absoluto de un número complejo coincide con la distancia euclídea desde el origen del plano a dicho punto.
Si el complejo está escrito en forma exponencial z = r eiφ, entonces |z| = r. Se puede expresar en forma trigonométrica como z = r (cosφ + isenφ), donde cosφ + isenφ = eiφ es la conocida fórmula de Euler.
Podemos comprobar con facilidad estas cuatro importantes propiedades del valor absoluto
para cualquier complejo z y w.
Por definición, la función distancia queda como sigue d(z, w) = |z - w| y nos provee de un espacio métrico con los complejos gracias al que se puede hablar de límites y continuidad. La suma, la resta, la multiplicación y la división de complejos son operaciones continuas. Si no se dice lo contrario, se asume que ésta es la métrica usada en los números complejos.
Argumento o fase
El argumento principal o fase de un número complejo genérico  (siendo x=Re(z) e y=Im(z)) viene dado por la siguiente expresión:
(siendo x=Re(z) e y=Im(z)) viene dado por la siguiente expresión:
 (siendo x=Re(z) e y=Im(z)) viene dado por la siguiente expresión:
(siendo x=Re(z) e y=Im(z)) viene dado por la siguiente expresión:
donde atan2(y,x) es la función arcotangente definida para los cuatro cuadrantes:
O también:  Siendo:
Siendo:
 Siendo:
Siendo:
la función signo.
Conjugado de un número complejo
Dos binomios se llaman conjugados si solo difieren en su signo central, por ejemplo, los dos binomios: 3m - 1 y 3m + 1 son conjugados.
El conjugado de un complejo z (denotado como 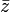 ó
ó 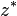 ) es un nuevo número complejo, definido así:
) es un nuevo número complejo, definido así:
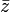 ó
ó 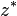 ) es un nuevo número complejo, definido así:
) es un nuevo número complejo, definido así:
Se observa que ambos difieren en el signo de la parte imaginaria.
Con este número se cumplen las propiedades:
Esta última fórmula es el método elegido para calcular el inverso de un número complejo si viene dado en coordenadas rectangulares.
Potencia de un número complejo
Para hallar la potencia de un número complejo, aplicamos el binomio de Newton. Teniendo en cuenta las potencias de la unidad imaginaria el resultado esotro número complejo cuya parte real es
y cuya parte imaginaria es
Precisamos, para llevar a cabo este cálculo de dos funciones auxiliares denominadas combinatorio y potencia, una que calcule en número combinatorio m sobre n, y otra que calcule el resultado de elevar un número real a una potencia entera.
Empezaremos por la más sencilla, la que calcula la potencia de un número real que será similar a la potencia de un numero entero que ya estudiamos. Para este propósito, se puede emplear la función Math.pow, que tiene dos parámetros del tipo double.
En el siguiente mapa podemos ver como se denomina y como se caracteriza los números complejos :
Vídeos Extra de explicaciones de ejercicios avanzados: